Elastic Shape Optimisation

An overview of the second project for the 2024 edition of CS-457 Geometric Computing at EPFL. Project was completed in collaboration with Shivang Sachar and Athanasios Charisoudis.

Introduction

We're in a garage, pouring hot rubber into a dinosaur mould. After cooling, we crack open the mould and a rubber dinosaur springs out. It flops and squishes under gravity, and doesn't look much like the original dinosaur.

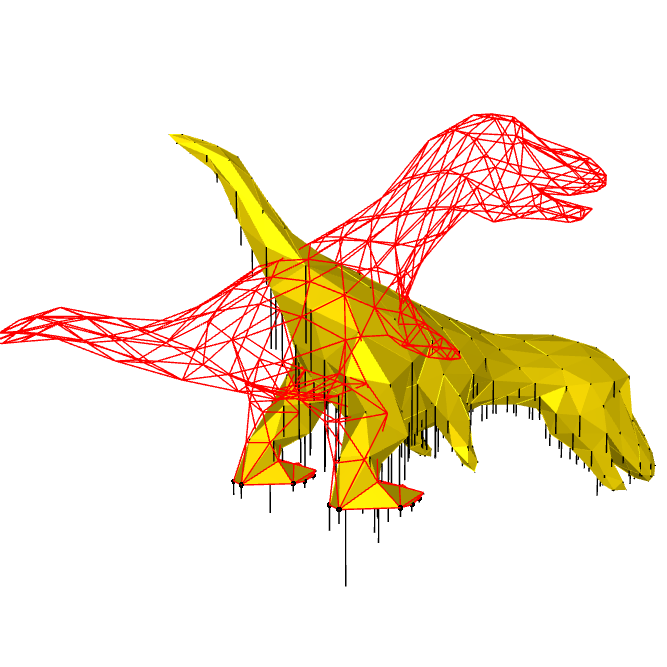
Problem statement

How should we design a mould, such that the deformed dinosaur matches the original model?

Part 1 - Forward Simulation

1.1 Static equilibrium

We need to figure out what the rubber dinosaur will look like when it settles into static equilibrium. That is, given a tetrahedral mesh description of the dinosaur, we need to design a computer programme that will return an updated mesh where the sum of forces is zero.

Let's call the dinosaur \(\Omega\subset \mathbb{R}^3\). There are two contending forces at play. On one hand, gravity will pull the dinosaur downwards. On the other hand, the internal elastic forces will pull the shape back up. We describe a deformation of the mesh with the function \(\Phi:\mathbb{R}^3\rightarrow\mathbb{R}^3\).

Since we do not need to simulate the entire deformation process, an energy description of the dinosaur is practical. Gravitational and elastic potential energies cumulate at each point of the dinosaur. To compute the static equilibrium state of the dinosaur, we iteratively update its tetrahedral mesh to minimize the total energy.

1.2 Elastic energy density - Material model

We assume that the material is hyperelastic and has homogeneous mass density. So it can't permanently deform or completely flatten, and when there is no deformation there are no elastic forces. Formally, the energy depends purely on the deformation \(\Phi\).

To compute the elastic energy in the dinosaur, let's step back from dinosaurs for the moment and think about Hooke's Law for 1D materials.

In order to local deformations are captured by the Jacobian \(\nabla \Phi \in \mathbb{R}^{3 \times 3}\)