Inverse Geometric Propulsion
TLDR: I wrote an algorithm to control the trajectory of shape-changing rockets.
Download the PDF.
Abstract
Controlling shape-changing bodies in zero-gravity is complex but critical for tasks like space robotics or animation. We extend a motion planning algorithm for shape-changing bodies to the control of non-zero momentum. By formulating physical motion as a energy-minimising trajectory on a configuration manifold, we enable the discovery of non-trivial, physically valid motion paths that combine shape change with momentum control. The use of a stable variational integrator for the forward simulation leads to an efficient optimisation algorithm. We validate our method on abstract mechanical systems such as rigid bodies and a hinged flap with thrusters. This approach can inform motion planning in space robotics, reinforcement learning, and procedural animation.
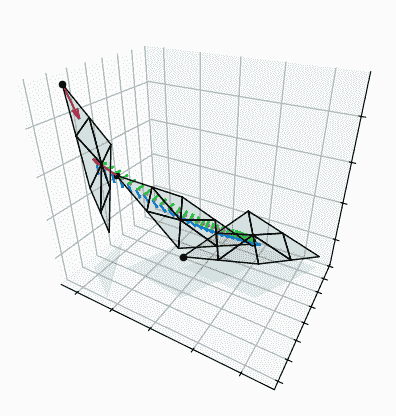
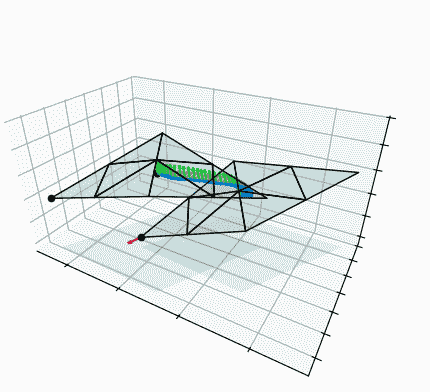
Example
This shape is meant to be an abstraction of a gimballed rocket engine. The idea is that it has a rocket pinned to the tip of one flap. The flap can open or close, which points the rocket up or down. Here I've set the objective for the flap to turn its whole body 90º about its hinge axis, which is only possible if it activates the rocket with good timing. The control algorithm efficiently computes the sequence of hinge angles and forces that together result in the 90º rotation.
Random ❌